стандартное отклонение для начинающих

1. Коэффициент вариации
2. Типичная область изменения
3. Пример средней зарплаты
4. Когда обращать внимание на стандартное отклонение?
5. Плюсы и минусы стандартного отклонения

Расчет среднего арифметического иногда слишком мало. Так что, если мы знаем среднюю заработную плату в компании (например, в нашем примере 5000 злотых), поскольку мы не знаем, какова изменчивость вознаграждения? Все ли сотрудники получают одинаковую сумму? А может, менеджер завышает значение средней зарплаты? Я приглашаю вас прочитать текст о стандартном отклонении. Это один из инструментов, который позволяет анализировать разброс значений вокруг среднего.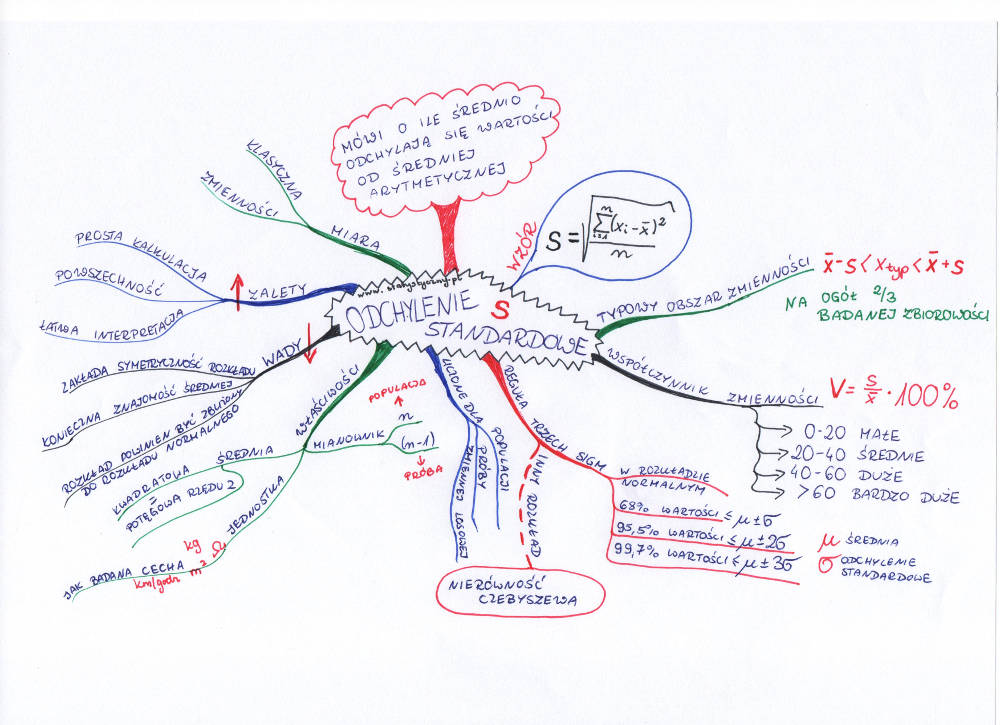

карта разума: стандартное отклонение

Стандартное отклонение говорит о том, насколько значения тестируемого признака отклоняются от среднего арифметического. Звучит как масло, но нет? В среднем, в среднем? Что это значит?

Я скажу тебе. Вы уже знаете разные средние: арифметический , гармоника и геометрический , И вот в чем фокус - стандартное отклонение не учитывается ни для одного из этих средних значений. Используется совсем по-другому - средняя площадь. Средним квадратом является средняя степень мощности 2 (средняя гармоника равна -1 градусу, геометрическая равна 0 градусам, арифметическая величина равна 1 градусу). И это среднее значение, необходимое для расчета стандартного отклонения. И как мы это делаем? Я опишу все сразу и покажу примеры. Я надеюсь, что тогда все будет понятно.

Сначала рассчитаем среднее арифметическое - оно нам скоро понадобится. Затем, в свою очередь, мы рассчитываем разницу между значением признака каждой наблюдаемой единицы и средним арифметическим. Затем мы возводим каждое из различий в квадрат и суммируем все вместе. Наконец, разделите на количество наблюдений и извлеките вторую степень из полученного результата. И таким образом мы рассчитали стандартное отклонение.

А теперь то же самое, но сохранено с использованием математической формулы:

\ (S = \ SQRT {\ гидроразрыва {\ sum_ {= 1} ^ {N} (X_ {я} - \ Overline {х}) ^ {2}} {п}} = \ SQRT {\ гидроразрыва {( X_ {1} - \ Overline {х}) ^ {2} + (X_ {2} - \ Overline {х}) ^ {2} + \ ldots + (X_ {п} - \ Overline {х}) ^ {2 }}}} {п \)

(поскольку это «стандартное отклонение для начинающих», я не буду объяснять подробности, но только в двух словах я упомяну, что если вы рассчитывали стандартное отклонение выборки, а не совокупности, то измените знаменатель n на (n-1))

Стандартное отклонение является классическим показателем вариации распределения. Мы считаем их, чтобы определить, в наших ли население Единицы похожи из-за изучаемой особенности, отличаются ли они существенно.

Давайте возьмем самый простой пример - у нас есть 3 числа: 1, 2 и 3. Среднее арифметическое этих трех чисел равно 2 (рассчитывается по формуле: \ (\ frac {1 + 2 + 3} {3} \)). Стандартное отклонение рассчитывается следующим образом:

\ (S = \ SQRT {\ гидроразрыва {(1-2) ^ {2} + (2-2) ^ {2} + (3-2) ^ {2} {3}}} = \ SQRT {\ гидроразрыва {1 + 0 + 1} {3}} = \ SQRT {\ гидроразрыва {2} {3}} \ approx0,82 \)

Коэффициент вариации

Поскольку мы уже знаем стандартное отклонение, мы можем рассчитать различные другие показатели дисперсии, например коэффициент вариации:

\ (V = \ гидроразрыва {s} {\ Overline {х}} * 100 \% \)

Если коэффициент вариации колеблется в пределах 0-20%, вариация населения невелика. Если он находится в пределах 20-40%, то говорят о средней дифференциации населения. В случае 40-60% существует широкий разброс. Однако когда коэффициент вариации превышает 60%, это означает, что вариация очень велика.

Для нашего примера три числа 1, 2 и 3 будут:

\ (V = \ гидроразрыва {0,82} {2} * 100 \% = 41 \% \)

Результат 41% означает, что разнообразие в нашем примере велико.

Типичная область изменения

После расчета стандартного отклонения и среднего арифметического, вы также можете рассчитать так называемый типичная область изменения:

\ (\ Overline {х} -s

В нашем примере:

\ (2-0,82

Это означает, что типичная область изменения колеблется от 1,18 до 2,82.

Упрощенно сказано, что типичная область вариации содержит 2/3 обследованного населения. Это упрощение, потому что оно учитывает неписаное предположение, что мы имеем дело с нормальным распределением или распределением, близким к нормальному (что это за нормальное распределение, тогда тема для более длинного утверждения, и я не буду временно объяснять). Я добавлю больше. Если наши данные получены от населения с нормальным распределением, то 68% населения находится в пределах одного стандартного отклонения от среднего арифметического. На расстоянии 2 стандартных отклонения учитывается 95,5% наблюдаемых единиц. Однако на расстоянии 3 стандартных отклонения учитывается 99,7% исследуемой популяции. Это очень важная информация, потому что многие статистические гипотезы основаны на них, и мы вернемся к этой теме много раз.

А что если мы знаем, что наше население не имеет ничего общего с нормальным распределением? Затем принимаются некоторые более строгие условия, вытекающие из неравенства Чебышева. Предполагается, что на расстоянии двух стандартных отклонений от среднего значения наблюдается 75% наблюдений, на расстоянии 3 отклонений - 88,89% наблюдений, на расстоянии 4 отклонений - 93,75% наблюдений, а на расстоянии 5 стандартных отклонений от среднего значения 96% наблюдений.

Пример средней зарплаты

И еще раз, давайте вернемся к нашему примеру со средней зарплатой:

1. "Wszystko Równo" - работает 10 сотрудников, каждый из которых получает 5000 злотых в месяц.
2. «Chief Mountain» - работает уборщицей, которая по контракту получает 500 злотых, включая 8 частных работников с зарплатой 1500 злотых, и менеджера, который получает 37 500 злотых ежемесячно.
3. «Только для продвижения по службе» - у нас также есть 10 сотрудников, пять из которых работают ниже года и получают 3000 злотых, остальные пять проходят более длительную практику, и благодаря этому они получают зарплату в 7000 злотых каждый.
4. «Wielka Niewiadoma» - десять сотрудников, каждый с разной зарплатой, от 1000 до 9000 злотых.

Напоминаю, что во всех приведенных выше примерах средняя заработная плата составляет 5000 злотых (рассчитывается с использованием среднего арифметического). И я доказываю, что информации о средней заработной плате недостаточно, чтобы осознанно выбирать, в какой компании мы хотели бы работать. Итак, давайте подумаем о вопросе стандартного отклонения, типичной области вариации (без учета предмета нормального распределения) и коэффициента вариации?

В компании «Równi Równo» стандартное отклонение составляет ровно 0. Коэффициент вариации также равен 0, и таким образом мы узнаем (только из информации о среднем арифметическом и стандартном отклонении), что все сотрудники зарабатывают одинаковую сумму.

В «Сефо Гура» ситуация совершенно иная. Стандартное отклонение составляет 10 837,44 злотых. Много, правда? И все благодаря одному управленческому вознаграждению. Коэффициент вариации здесь превысил 200%. 10837,44 / 5000 * 100% = 216%. Типичная область волатильности достигает отрицательной заработной платы. Мне кажется, что это хороший пример, чтобы избежать классических показателей как положения (среднее арифметическое), так и изменчивости (стандартное отклонение) в ситуациях, когда мы имеем дело с большими экстремальными значениями. Я напоминаю вам, что медиана как хорошо межквартильный размах (то есть измерения положения) очень хорошо показали, какое вознаграждение мы можем ожидать в этой компании.

В случае «Byle do Upward» стандартное отклонение составляет 2000 злотых. Коэффициент вариации составляет 40% (т.е. зарплата находится на границе средней и высокой волатильности), а типичная зарплата, которую должны получать не менее 2/3 работников, составляет от 3000 до 7000 (в нашем случае каждый получает ровно 3000 злотых или 7000 злотых) ,

А также компания "Wielka Niewiadoma". Здесь стандартное отклонение вознаграждения составляет 2459,67 злотых. Коэффициент вариации составляет 49% (то есть изменчивость вознаграждения высока), а типичное вознаграждение 2/3 работников находится в диапазоне от 2540,33 зл. До 7459,67 зл.

Еще одна мера - дополнительная информация. Вы уже знаете, в какой компании хотели бы работать?

Когда обращать внимание на стандартное отклонение?

Стандартное отклонение используется (или, по крайней мере, часто) в повседневной жизни. Он рассматривается, среди прочего, как мера риска в случае инвестиций. Если на бирже одна компания приносила среднегодовую прибыль 4%, а вторая среднегодовая прибыль 5%, это не значит, что лучше выбирать вторую компанию, не задумываясь. Помимо фундаментального анализа и технического анализа для конкретной компании, помимо макроэкономической ситуации в стране, стоит обратить внимание на колебания котировок. Если стоимость акций первой компании в течение года имела незначительные колебания в несколько процентов, а у второй она колебалась на несколько десятков процентов, то логично, что инвестиции в первую компанию были гораздо менее рискованными. А для сравнения разных ставок доходности и проверки их рискованности можно использовать стандартное отклонение. Чем выше стандартное отклонение, тем рискованнее инвестиции.

Также обратите внимание, что информация о среднегодовой температуре в данном городе мало что нам скажет. В Польше у нас четыре сезона, температура между летом и зимой совершенно разная. Однако есть страны, где температура колеблется незначительно в течение года. Даже если среднегодовая температура сравнима, это не значит, что речь идет об одном и том же климате. Здесь вы также можете использовать стандартное отклонение (или другие меры отвлечения ) чтобы проверить, изменяются ли температуры от средней до очень маленькой.

Плюсы и минусы стандартного отклонения

Каковы преимущества стандартного отклонения? Прежде всего, он широко используется, все знают, что это и откуда. Стандартное отклонение рассчитывается довольно легко (несмотря на эти жестокие суммы и элементы в формуле) и даже легче интерпретируется. Статистика используется очень часто. Если вы хотите поближе познакомиться со статистикой, вы также хотите подружиться со стандартным отклонением. И вы должны простить его за те недостатки, которые он также имеет. И среди них наиболее важным является то, что он предполагает симметрию распределения. Стандартное отклонение считается наилучшим, когда в нашем исследовании популяция имеет нормальное распределение (или хотя оно близко к нормальному). И не забывайте, что для расчета стандартного отклонения сначала нужно вычислить среднее арифметическое.

Пожалуйста, следуйте и нам нравится:

Похожие

Комментарии