Как рассчитать стандартное отклонение выборки и популяции?

1. Несколько слов, чтобы напомнить вам, что такое стандартное отклонение
2. Стандартное отклонение от образца
3. Пример - когда стандартное отклонение выборки и когда популяции
4. Таблицы и стандартное отклонение
5. суммирование

«Помогите, помогите! Я считаю стандартное отклонение в Excel (или другой электронной таблице), и результат получается совершенно другим, чем я рассчитывал на калькуляторе, на листе бумаги или просто в моей голове. Где ошибка сидит, потому что я проверяю пятый раз, и она все равно выходит? "

Регулярные читатели статистики уже знают, что запись о стандартное отклонение это было давно, и они могут рассчитать такое отклонение. Но даже тогда я упомянул только что-то вроде стандартного отклонения от попытки , И подсчет именно такого отклонения должен быть осторожным, потому что схема отличается от стандартного отклонения в население ,

Несколько слов, чтобы напомнить вам, что такое стандартное отклонение

Напомним в начале, что такое стандартное отклонение. Это мера изменчивости распределения, которая он говорит о том, насколько значения проверяемой функции отклоняются от среднего арифметического. Большое стандартное отклонение информирует нас о том, что население очень разнообразно, а небольшое стандартное отклонение говорит о том, что отдельные единицы близки к среднему. Узор, напомню, выглядит так:

\ (S = \ SQRT {\ гидроразрыва {\ sum_ {= 1} ^ {N} (X_ {я} - \ Overline {х}) ^ {2}} {п}} = \ SQRT {\ гидроразрыва {( X_ {1} - \ Overline {х}) ^ {2} + (X_ {2} - \ Overline {х}) ^ {2} + \ ldots + (X_ {п} - \ Overline {х}) ^ {2 }}}} {п \)

Стандартное отклонение от образца

Вот как это выглядело в случае с населением. И как это будет выглядеть в случае судебного разбирательства? В паттерне мы имеем дело с одним маленьким крошечным изменением. А именно, в знаменателе дроби вместо n появляется (n-1) .

\ (S = \ SQRT {\ гидроразрыва {\ sum_ {= 1} ^ {N} (X_ {я} - \ Overline {х}) ^ {2}} {п-1}} = \ SQRT {\ гидроразрыва {(X_ {1} - \ Overline {х}) ^ {2} + (X_ {2} - \ Overline {х}) ^ {2} + \ ldots + (X_ {п} - \ Overline {х}) ^ } {2} {п-1}} \)

Что означает это изменение? На практике стандартное отклонение, рассчитанное по выборке (в случае тех же данных), будет немного больше, чем отклонение популяции. Чем больше выборка, тем больше будет размыт разрыв. В случае небольших выборок, особенно довольно разнообразных, изменение значения n на ( n-1 ) может существенно изменить результат.

Откуда разница в шаблонах? Почему ( n-1 )? При расчете стандартного отклонения образца можно ли использовать первую формулу только с n ? Помните, что, считая стандартное отклонение выборки, мы рассчитываем неизвестный параметр. Мы оцениваем значение стандартного отклонения для населения. Проще говоря, мы можем сказать, что мы знаем, что мы не знаем ни истинного среднего населения, ни истинного стандартного отклонения. Поэтому мы ожидаем, что истинное стандартное отклонение для населения будет отличаться от выборки (хотя бы потому, что мы используем расчетное среднее значение для его расчета, а не реальный параметр для всей популяции). И ожидая эту разницу, мы принимаем большее значение отклонения. Но если мы не планируем оценивать, то нам не нужно использовать формулу для статистической выборки. Итак, когда мы можем использовать формулу, в которой только n подсчитывает стандартное отклонение выборки? Затем, когда мы сознательно подсчитываем значение отклонения только для этой выборки и не планируем обобщать результат для всей совокупности. Мы не рассматриваем это как оценку для населения, но мы считаем параметр из выборки.

Пример - когда стандартное отклонение выборки и когда популяции

Теория Теория. Испытания, популяции, n , n-1 . Все перепутано, и трудно почувствовать это. Я думаю, что будет лучше, когда нам поможет сладкий пример:

1. Я купил 20 печенья, и я хочу знать, сколько они весят и каково стандартное отклонение веса моих печенья. Меня интересуют только мои купленные печенья. Поэтому я использую первую формулу для стандартного отклонения в популяции.
2. Я купил точно такие же 20 печенья, но я хочу знать, сколько они весят и какое стандартное отклонение они имеют для всех тортов из моих любимых кондитерских изделий. Я хочу знать, какова вероятность того, что в следующий раз я получу печенье большего или меньшего размера. Затем я использую вторую формулу для стандартного отклонения от образца.
3. Я владелец кондитерской. Я взвешиваю и измеряю все печенье. Я могу точно сказать, каков средний вес печеного печенья. Я также могу рассчитать стандартное отклонение для всех файлов cookie. Я снова использую первую формулу для стандартного отклонения в популяции.

Таблицы и стандартное отклонение

И теперь мы приходим к тому, что было в начале. Наиболее распространенное использование в электронных таблицах функций «стандартное отклонение» или «стандартное отклонение» совершенно не осознает, что оно относится к стандартному отклонению выборки. Если мы хотим вычислить отклонение для совокупности, то мы должны использовать функцию «stdevp» или «стандартное отклонение» (примечание! В разных таблицах эти имена могут различаться - я настоятельно рекомендую вам внимательно прочитать описание функции перед использованием). Самая частая ловушка - это ручное вычисление стандартного отклонения для населения, и для проверки результата используйте функцию «stdev» на листе. Вот когда появляются различия и повторения - где мы можем пойти не так? Чтобы не дать себя одурачить - каждый раз стоит прочитать, что именно означает функция, которую мы намерены использовать.

суммирование

Я намеренно не упоминаю, что, считая стандартное отклонение выборки и используя формулу с одним n, мы должны были бы иметь дело со смещенной оценкой. Я не упоминаю, что ( n-1 ) означает несмещенную оценку отклонения (или стандартное отклонение также?). Я не упоминаю степени свободы и т. Д. Возможно, однажды я займусь записью, которая объяснит эти сложности, но на данный момент все те, кто больше интересуется этой темой, ссылаются на типичные умные учебники из статистики. И не удивляйтесь, если вы прочитаете где-нибудь, что все это было изобретено давно, и это действительно не имеет значения, если вы считаете n или n-1 . Иногда получается, что в статистике не все вопросы имеют только один очевидный ответ. И статистики могут также иметь разные мнения о том, когда использовать дизайн.

Чтобы напомнить себе, что уже было в статистике - я призываю вас использовать это оглавление , Быть в курсе событий - это нравится facebook , И лучше всего убедить нескольких коллег сделать это - потому что почему они устают только от статистики учебников, если вы можете усвоить ее в более приятной версии?

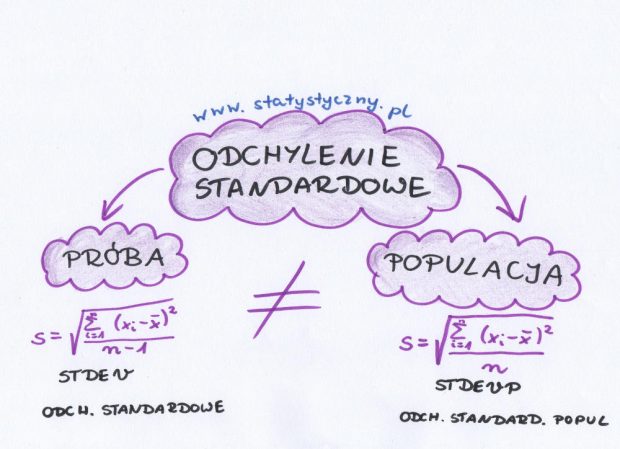
карта разума: стандартное отклонение выборки

Пожалуйста, следуйте и нам нравится:

Похожие

Комментарии