в среднем еж или среднее арифметическое

У меня сложилось впечатление, что наиболее известным статистическим понятием является среднее арифметическое . Конечно, все слышали много раз, сколько у них средняя зарплата, они подсчитывали средний балл в школе, или он задавался вопросом, каков средний расход топлива в машине.

Что такое среднее значение и как его можно рассчитать? Его значение всегда очевидно?

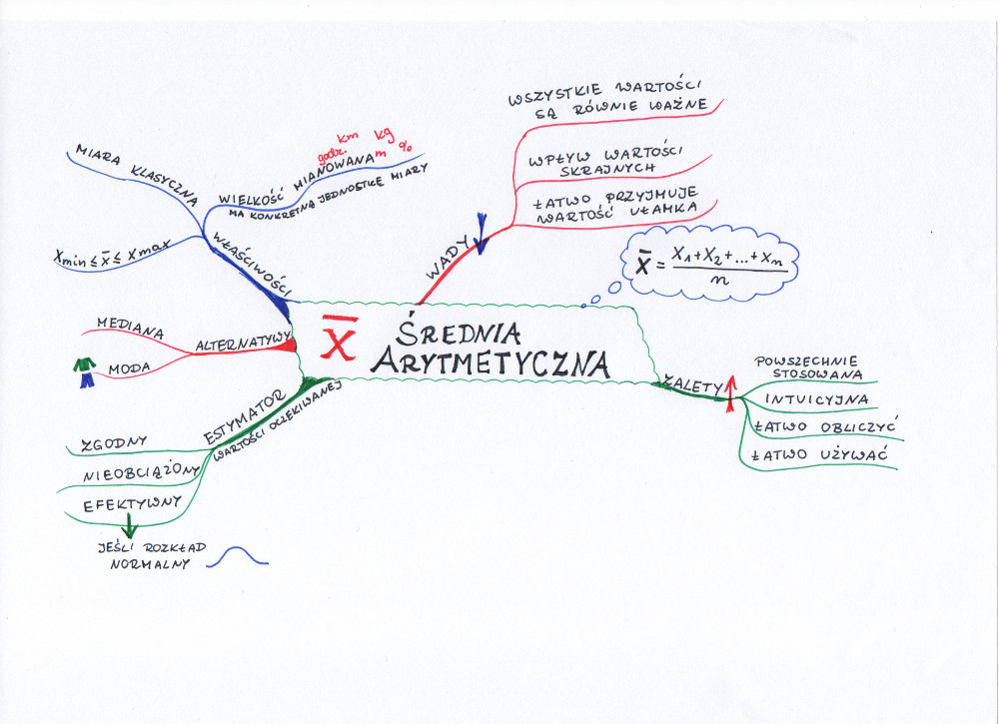
Карта разума: среднее арифметическое

Среднее арифметическое получается путем суммирования значений всех проверенных объектов и деления этой суммы на количество объектов.

\ (\ Overline {х} = \ гидроразрыва {X_ {1} + X_ {2} + ... X_ {п} {т}} \)

Самый классический пример, известный из начальной школы, - это подсчет средней оценки. У нас есть пять предметов: польский, математика, английский, природа и физическое воспитание. Студент получил следующие оценки в конце семестра, соответственно: 4, 5, 2, 4, 5. Как мы рассчитываем среднее арифметическое? Путем добавления друг к другу отдельных оценок (4 + 5 + 2 + 4 + 5), а затем деления на количество предметов. 20/5 до 4. Таким образом, наши расчеты показывают, что класс ученика равен 4.

Как видно из примера, среднее арифметическое рассчитывается очень легко, особенно когда у нас есть доступ ко всем значениям. Он интуитивно понятен, легко интерпретируется, прост в использовании и благодаря этому широко используется - к сожалению, также в ситуациях, когда это не нужно.

Недостатки среднего арифметического

Среднее арифметическое имеет несколько основных недостатков, которые стоит отметить:

1. Прежде всего, это большое влияние экстремальных ценностей. Давайте предположим, что мы хотим продать книгу об Allegro и проанализировать цены продажи из прошлого. Если в большинстве случаев цена книги составляла 20-25 злотых, и в то же время один экземпляр шел за 2000 злотых (поскольку он имел автограф автора и был куплен страстным поклонником), сумма в 2000 злотых значительно увеличит среднюю стоимость книги.
2. Среднее легко принимает значения дроби, даже в ситуациях, когда дробное значение никогда не имеет права встречаться в реальности. Например, коэффициент рождаемости, который для Польши в 2013 году составил 1,32 и является числом рожденных детей на одну женщину детородного возраста. С одной стороны, мы знаем, как интерпретировать это число (о, к сожалению, мало местных детей), но в то же время мы понимаем, что нет женщины, которая родила бы 1,32 ребенка.
3. Все значения одинаково важны и одинаково влияют на результат. Если наша цель состоит в том, чтобы проанализировать элементы, которые меняются со временем, и мы хотели бы дать новым значениям наибольшую ценность, то, к сожалению, среднее арифметическое не будет полезным. Давайте вернемся к примеру продажи книги на аллегро. Если у нас есть данные о ценах за последние 5 лет, мы можем включить все значения, но в то же время придать больший вес суммам за прошлый год. В этой ситуации обычное арифметическое среднее не найдет своего применения.

Пример собаки

Вы слышали известное высказывание, что, поскольку у меня две ноги, а у моей собаки четыре, в среднем у нас три ноги. На нем часто говорят люди, которые не понимают статистику, не знают, когда ее использовать и как использовать рассчитанные значения. Это чтобы показать, что статистика искажает реальность. Это предложение является наиболее верным. Мы суммируем 2 + 4 и получаем 6. Затем мы делим на количество единиц, которые мы изучаем (2), и, по сути, результат получается 3. Но был ли это результат, который мы хотели получить? Нас интересует среднее количество ног одной собаки и одного человека? Они должны представлять всех собак и всех людей? Жители нашего жилого комплекса? Или все млекопитающие на земле? Почему мы считаем средние ноги двух совершенно разных существ?

Отойдя от предмета (для полных мирян - пожалуйста, не паникуйте!) Предмет стандартного отклонения и типичной области вариации появится в ближайшее время - пока, относитесь к нему с расстоянием) , стоит не только смотреть на среднее значение, но и другие меры, которые в некотором роде они связаны с этим. Например, стандартное отклонение. В нашем случае собаке и мужчине ровно 1. Пойдем дальше. Типичная область изменения, в которой приблизительно 2/3 объектов теоретически расположены (при определенных допущениях, конечно), находится в диапазоне от 2 до 4 (мы вычитаем стандартное отклонение из среднего арифметического для получения нижнего предела и добавляем стандартное изгибание для получения верхнего граница). Ну и что? Таким образом, наша собака и ее владелец вписываются в типичную область изменчивости. С нашей статистикой все не так плохо, хотя бессмысленный пример и наши расчеты могут только опровергнуть не очень умный аргумент о том, что статистика плохая.

(Кстати - интересный текст о примере трех ног человека и собаки тоже можно найти здесь .)

Пример средней зарплаты

Теперь давайте перейдем к чему-то более полезному. Компания набирает сотрудников и, в качестве одного из побудительных аргументов, заявляет: «Средняя зарплата в нашей компании составляет 5000 злотых». Звучит заманчиво, правда? Но достаточно ли этой информации для нас? Он скажет нам, сколько будет на самом деле наш заработок?

Давайте предположим, что у нас есть четыре компании:

1. "Wszystko Równo" - работает 10 сотрудников, каждый из которых получает 5000 злотых в месяц.
2. «Chief Mountain» - работает уборщицей, которая по контракту получает 500 злотых, включая 8 частных работников с зарплатой 1500 злотых, и менеджера, который получает 37 500 злотых ежемесячно.
3. «Только для продвижения по службе» - у нас также есть 10 сотрудников, пять из которых работают ниже года и получают 3000 злотых, остальные пять проходят более длительную практику, и благодаря этому они получают зарплату в 7000 злотых каждый.
4. «Wielka Niewiadoma» - десять сотрудников, каждый с разной зарплатой, от 1000 до 9000 злотых.

В каждой из вышеперечисленных компаний среднее вознаграждение составляет 5000 злотых. Конечно, не в каждом из них мы хотели бы работать. В таком случае среднее вознаграждение абсолютно недостаточно.

Пример - мешки с мукой

После этих двух примеров, которые показывают, насколько несовершенным является среднее арифметическое, я хотел показать ситуацию, когда использование среднего значения оправдано. Предположим, у нас есть мельница, в которую мы загружаем муку в килограммовые мешки. Что ж, после целого дня мы хотели бы проверить, действительно ли в мешках оказался килограмм муки. Поэтому мы взвешиваем все мешки с мукой, и получается, что только некоторые весят ровно 1000 грамм. Есть сумки, которые легче и тяжелее. Но как узнать, добавили ли мы слишком много или слишком мало? Расчет среднего арифметического будет полезен здесь. Мы интуитивно догадываемся, что имеем дело с однородным сообществом, в котором не должно быть слишком много экстремальных ценностей (не так ли?) - это также стоит проверить), все ценности так же важны для нас, и результат в форме доли из нас это вас не беспокоит. Таким образом, все основания для использования среднего арифметического значения выполнены.

Есть ли у вас идеи, когда вы должны посчитать среднее арифметическое, а когда его значение не имеет смысла? Может быть, несколько примеров? Я призываю вас поделиться в комментариях.

И мой пример реального и повседневного использования среднего арифметического появится в следующей записи. Я приглашаю вас прочитать.

Пожалуйста, следуйте и нам нравится:

Похожие

Комментарии